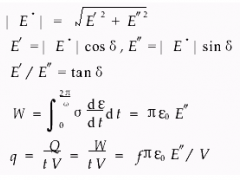朱永康 (中橡集团炭黑工业研究设计院,自贡 643000) 编译
填料网络化对填充橡胶料的形态学和性能有巨大的影响。这种填料网络化取决于填料的分散状态,而后者又会直接影响滚动阻力、牵引性、胎面耐磨性和汽车轮胎中的机械性能。炭黑在橡胶中的分布是受混炼过程支配的,在此过程中炭黑粒子在剪切条件下分散到整个聚合物基质当中。随着填料配合量的增加,填料粒子之间的接触加大。当其达到一定的配合量时,填料就会形成一种可以在渗透阈理论或团簇-团簇聚集理论框架内描述的连续网络。从Payne和其他人早先的工作中,可以发现橡胶胶料内填料网络存在的证据。据认为,对于给定的橡胶和硫化体系,填料网络化是支配填充橡胶动力学行为的主要因素。从热力学角度讲,填料网络化的驱动力乃是填料和聚合物之间表面能的差异。其表面能的差异越大,聚合物和填料之间的相互作用越小,聚合物中的网络化趋势越大。而这样的填料网络化,是通过偏好自我聚集或絮凝的填料形成三维网络的性质来实现的。这会导致影响胶料物理性能的粘度和模量的急剧增大。
图1示出典型的白炭黑填充橡胶胶料(未加硫化剂)在160℃的絮凝行为,可以看出小应变模量随着后热处理时间增加而增大。这些数据是利用橡胶加工分析仪获得的,表明了正如小应变模量所检测的那样,硬度在热处理期间明显增大。这表明粒子发生了相对运动,填料网络的形成取决于粒子的尺寸、聚合物的种类以及聚合物-填料间的相互作用和填料-填料间的相互作用。图1中的符号为实验数据,线条为拟合曲线,证明分别通过具有短松弛时间t1和长松弛时间t2的两个指数过程之和,很好地描述了絮凝现象。
在本研究中,我们从絮凝行为和应变诱发的填料网络断裂等方面对填充橡胶体系进行了考察。在流变条件下研究了稳定剪切对填料网络断裂的影响,进而研究了填料网络在熔体流当中的作用。

1 实验部分
1.1 材料
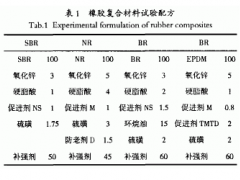
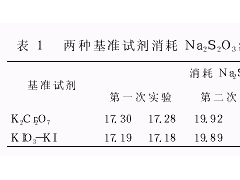
本研究使用的橡胶为市售品级。其化学特征性能示于表1,该表中还列出了聚合物中有重要热力学意义的乙烯基链段和苯乙烯单元质量分数。采用N330炭黑品种作为填料。

为了制备填料补强橡胶复合材料,分别将EPDM与30份炭黑和35份炭黑混合,S-SBR与35份炭黑和40份炭黑混合。这些体系于60℃在1.5L捏炼机内与3份氧化锌、2份抗氧化剂和1份硬脂酸捏炼。先让聚合物预混炼2min,然后加入炭黑和其他配合剂。
1.2 高压狭缝毛细管流变仪与介电宽带光谱术的组合
流变仪中有一根狭缝毛细管,两根电极固定于与狭缝平行的毛细管内。电极与毛细管壁是绝缘的。将这两根电极与频率响应分析仪相连接,以便进行介电测定。实验在100℃的温度下进行。活塞速度由0.0001mm/s变为0.4mm/s,并在流变仪内按不同的活塞速度获得剪切速率。用3个压力传感器来探测包括1000、700和350 Pa的压力降,这些传感器的安装与毛细管的狭缝保持平行。当流体以一定的活塞速度趋于恒定时,在10-1~106Hz的频率范围内进行介电测定。与介电宽带光谱仪相连的高压狭缝毛细管流变仪的实验装置示意图见图2。

2 介电函数ε*和σ*的评估
对于介电常数的变化,材料的导电率因为电流I*(在交变电场中是复数量)而变得与频率相关,等于电容器充电Q*的变化,并由此变成了电容C*和电压U*的一阶导数的乘积。此外,通过用C*=ε*ε0F/d和U*=E*d来代替电容(这里ε*为复数介电常数,ε0为真空介电常数,F为垂直于电场的试样面积,d为平行于电场的试样厚度),电流就可以表示为复数介电常数的函数(库仑定律):
I*=(dQdt)*=C*dU*dt=ε0ε*dE*dtF(1)假设E*=E0eiωt,可获得
dE*dt=E0eiωtiω=iωE*(2)故有
I*=ε0ε*iωE*F(3)
电阻R*可以用导电率σ*表示为(欧姆定律):
R*=1dσ*F=U*I*=E*dII*(4)
如果遵循导电率的表达式σ*=ε0ε*iω(5)
根据公式(6)分为实际的介电常数和假想的介电常数:
ε*=ε′-iε″(6)则:
σ*=σ′+iσ″=ε0ε″ω+ε0ε′iω(7)故有
σ*=ε0ε″ω(8)
和σ*=ε0ε′ω(9)
显然,通过复合介电常数ε*描述的材料,其介电松弛会强烈影响复合电容率ε*的实际部分和假想部分。

3 剪切流对橡胶熔体内填料团簇解体的影响
填充30份炭黑的EPDM在不同温度时,其粘度和剪切应力随剪切速率的变化示于图3。显而易见,粘度随着温度及剪切速率的增加而降低,具有-0.7指数的幂律行为由此得到了充分的证明。图4中示出100℃下无交联剂时同一种胶料的导电率对剪切速率的相应的依赖关系。该实验是流动状态下在高压毛细管流变仪内进行的。可以看出,对于所有的剪切速率,低频导电率(它等于直流导电率的平台段)随着剪切速率的增大而降低。由于炭黑具有导电的性质,通过介电宽带光谱术就能在很宽的频率范围内探测出填料网络的破坏情况。在范围甚宽的导电率和电容率水平中能够看到这样的变化。

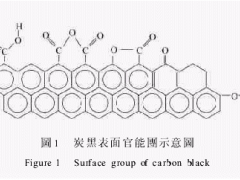
在孤立的聚合物基质中,电荷载体会追循导电填料网络的路径运动。炭黑聚集体间的导电并不需要两个原生聚集体间的接触,而仅仅只需要几个纳米级别的靠近即可。对于相邻聚集体间的纳米级缝隙,电荷迁移缘于量子力学隧道效应或电子的热激活跳跃。在临界配合量(此时p=Pc电子渗透阈)这种情况特别明显———炭黑聚集体在此形成通过试样的电子传导键闭合通道。这种绝缘体-导体过渡通过渗透阈理论可很好地解释。正如从图4(a)可看到的那样,导电率降低可能与填料网络的减少或填料团簇的解体有关。在8.1×10-3s-1的低剪切速率下,聚集体的平均分隔距离很小,如此一来就造成了导电率相当大(10-5Scm-1)。随着剪切速率的增加,聚集体发生了破坏,聚集体的平均距离增大,造成导电通道急剧减少,进而使得导电率陡然降低。当剪切速率由8.1×10-3s-1增加到29.4 s-1时,导电率由10-5下降至10-10Scm-1,可清楚地看出这一点。一旦施加剪切应力,填料网络随即便发生了破坏。

如图4(B)所示,介电电容率还会随着剪切速率的增大而降低。低剪切速率时的高电容率值与橡胶熔体内杂乱的、絮凝的填料形态有关。介电电容率描述在炭黑-弹性体界面处形成的极性化,在更低的频率视为Maxwell-Wagner极性化处理。可是,与球形粒子或椭圆形粒子相反,在导电性渗透团簇场合,极性化发生于最大团簇尺寸内的所有长度级范围,导致了观察到的电容率值异乎寻常的大(ε≈103)。这与炭黑网络的自相似性质有关。因此,当发生因剪切引发的填料团簇的破坏时,预期电容率将会下降。除剪切速率较小时的行为外,这是与图4中的实验发现相吻合的。观察到的电容率起初随着剪切速率提高的增大,或许与粒子及粒子团簇的相对运动有关。这无法通过基本的渗透或团簇-团簇聚集(CCA)模型来描述,而需要考虑动力学对剪切流下炭黑复合材料中电荷迁移的影响。
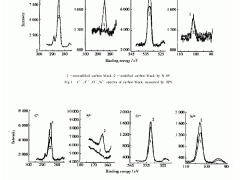
在图5所描绘的S-SBR中,随着剪切速率的增大,不同种类的炭黑网络发生了重排。在这里,处于非剪切状态时导电率水平低,在低剪切速率下导电率开始增大,在更高的剪切速率下则降低了。导电率水平起初在低剪切速率下的增加是填料发生絮凝的标志,这似乎得到了适中的剪切流的支持。在最低的剪切速率(7.91×10-3s-1)下,低频率处的导电率平台位于10-11Scm-1处,这就表明该体系低于渗透阈,并且填料团簇较小。当增大剪切速率时,导电率水平由于聚合物链的活动度增大而提高,这为相邻填料粒子或粒子团簇的聚集提供了佐证。随着剪切速率的增大,聚合物基质内的应力显著增加并超过了临界应力,絮凝的填料团簇又开始解体。由于填料聚集体间平均距离的增加,这招致了随后导电率平台的降低。
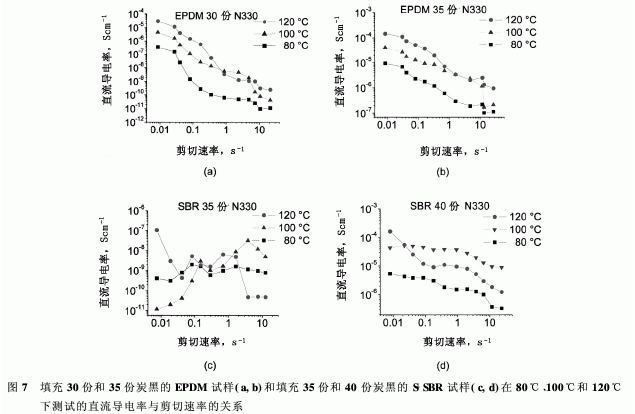
电容率低于及高于渗透阈的不同定性状况可能与临界剪切速率或剪切应力相关,填料团簇在达到渗透阈时开始解体。文献表明,根据较大的指数2+df,B(df,B≈1.8)是(CCA)团簇的主链分维的幂定律,相应的临界破裂应力随着团簇尺寸的增加而增大。但是,即使对于更大的指数3+df,B团簇应变也会增大,导致团簇的临界尺寸反过来依赖于橡胶基质周围的外加应力。因此,较大的团簇比较小的团簇更容易破坏,团簇的尺寸增加,临界剪切应力减小。这可以定性地解释为什么高于渗透阈时,呈现出大的炭黑团簇的EPDM试样在团簇出现破裂处表现出更小的临界剪切应力。相反,S-SBR试样在低于渗透阈时仅呈现出小的团簇,这些团簇在较大的剪切速率解体,导致导电率在高剪切速率下降低。当填料配合量增加到40份时(图6),发现最低的剪切速率(9.13×10-3s-1)其导电率平台大约为10-4Scm-1。这就表明该体系处于渗透阈之上。因而,在适中的剪切速率(≈10-1s-1)下临界剪切应力低,导电率随着剪切流的增大而开始降低。虽然在更高的剪切速率下填料团簇继续发生解体,导电率平台却仅降低了不到10个单位。这说明由于相对较高的填料配合量,聚集体间的距离非常小,流动引起的传导键破坏和重构对导电率的影响并不明显。图7示出了炭黑含量分别为30份和35份的EPDM和炭黑含量分别为35份和40份的S-SBR,推算的直流导电率平台随剪切速率变化的情形。对于EPDM而言,导电率水平随剪切速率的增加而同步降低,清楚地表明了填料网络在剪切流状态下发生破坏的现象。对于这些体系,观察到在整个剪切速率范围内导电率水平随着温度增加而提高,说明电荷迁移是通过电子在相邻炭黑聚集体间的纳米级缝隙的热激活跳跃发生的。填充35份炭黑的S-SBR的变化表明,填料的配合量尚未达到渗透阈。在这里,数据的离散性很大,无法观察到明显的趋势,尽管从总体上来看,120℃时的行为似乎与100℃和80℃时的行为并不相同。在120℃时,从导电率水平的降低可再次看到填料网络的破裂,这就说明在高温下发生了絮凝。对于填充40份炭黑的S-SBR观察到了与EPDM体系相似的趋势,因为这种复合材料又超过了渗透阈。
4 总结和结论
本文考察了絮凝对炭黑填充EPDM体系和S-SBR体系的影响。小应变模量随着热处理时间的增大表明了填料网络对胶料的硬度(和粘度)的影响。正如在剪切状态下的介电测定所检测到的那样,这与填料絮凝和橡胶熔体破裂的影响不相上下。在较低的剪切速率下,填料团簇相对要大些,这就导致了更低频率下的高导电率水平。在增大剪切速率时,通过导电率和电容率水平的下降即可探测出填料网络的破坏。在渗透阈之上,诸如此类的破裂,两种橡胶体系(即含30份及35份炭黑的EPDM和含40份炭黑的S-SBR)看上去都很清楚。而对低于渗透阈的体系也就是含35份炭黑的S-SBR,则观察到了相反的行为———即导电率和电容率随着剪切速率而增大。这一现象可能与炭黑粒子和团簇在剪切流中的相对运动有关,它会影响到填料网络破坏时反方向的介电响应。