关兵峰,马国富,魏荣梅,陈兵勇(中国航天科技集团四院四十二所,湖北襄樊441003)
摘要:该文研究了炭黑分散程度对橡胶疲劳性能的影响,利用SEM(扫描电子显微镜)研究了橡胶疲劳前后炭黑形态的变化。从断裂力学理论角度,提出了一种基于炭黑分散程度对橡胶疲劳寿命影响的橡胶疲劳破坏模型,结合已报道过的实验对此模型的合理性进行了分析。
关键词:炭黑分散程度;疲劳;模型
中图分类号:TQ 330.1+3 文献标识码:B 文章编号:1671-8232(2011)06-0020-04
橡胶制品具有独特的高弹性因而在各种减振领域有着广泛的应用,了解橡胶材料的疲劳破坏机理有助于人们设计出疲劳寿命更长的橡胶材料[1]。目前,被人们广泛接受的疲劳机理主要是断裂力学理论及唯象理论[2]。尽管出发点不同,但这二种理论均认为疲劳破坏源于外加因素的作用,使橡胶内部的微观缺陷或薄弱处逐渐遭到破坏。由于橡胶材料的疲劳寿命受多种因素的影响[3],破坏机理可能大相径庭,本文从炭黑分散程度对疲劳寿命影响的实验出发,借助SEM(电子显微镜)研究了橡胶疲劳前后微观结构的变化,综合文献中报道的一些实验,提出了一个基于炭黑分散程度对疲劳性能影响的橡胶疲劳破坏模型。
1·实验
1.1基本配方及试样制备
胶料基本配方:NR,100;促进剂CZ,1.5;促进剂M,1.2;硫磺,2;防老剂D,2;硬脂酸,2.5;氧化锌,5;N330,50。原材料牌号及产地为天然橡胶,标准胶5#,云南农垦产品;炭黑,N330,龙星炭黑公司产品;其他配合剂均为市售工业品级。
使用XK160型开炼机按常规步骤制备混炼胶,硫化条件为:160℃×t90×20 MPa,试片放置24 h后进行疲劳寿命测定。
1.2仪器及性能测试
疲劳寿命使用江都明珠实验机械厂生产的立式疲劳试验机测定试样的定伸疲劳,测定条件:温度25℃;80%定伸;频率,4 Hz。
混炼胶应变扫描采用美国TA公司生产的ARES高级扩展流变仪进行测试,测试条件:温度80℃,频率1 Hz,试样厚度为2±0.1 mm。采用日本JSM—6030LV型SEM,在试样新切出的断面表面喷金后进行观察,疲劳后试样切面与拉伸方向平行。
2·疲劳模型的提出
2.1炭黑分散程度对橡胶疲劳寿命的影响
根据Palmegren的观点[4],填料与橡胶的混炼工艺可分混入、分散、混合和塑化四个阶段。通常使用开炼机进行混炼的步骤为:生胶使用小辊距薄通使之包辊后,逐步放大辊距,加入各种配合剂进行混炼。待胶料吃粉完毕后再进行薄通使填料均匀分散。混入阶段可理解为橡胶在较大辊距下的“吃粉”过程。因此,可以通过控制薄通次数来获得不同分散程度的样品,制备大批混炼胶至吃粉结束后,将其分为八份,每份进行X遍薄通后编号FX,对不同薄通次数的样品进行应变扫描,结果如图1所示。
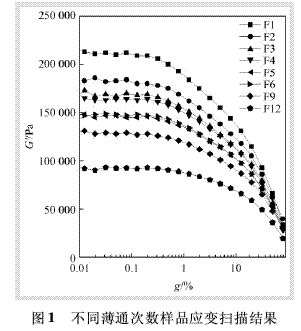
炭黑在橡胶中的理想分散状态为一次聚结集体分散,但通常都达不到理想的分散而含有大量二次聚集体。Payne研究发现[5],当对炭黑填充混炼胶施加一定的剪切变形后炭黑二次聚集体会发生破坏,导致混炼胶剪切模量骤降,这就是著名的Payne效应。炭黑分散越差,二次聚集体含量越高,则模量下降幅度越大,因此,该效应也可以用来表征填料分散程度。从图1可以看出,随薄通次数的增加,模量下降幅度变小,说明炭黑分散趋好。图2为薄通次数与疲劳寿命之间的关系。从图中可以看出,随薄通次数的增加,炭黑分散程度提高,天然橡胶疲劳寿命也显著延长。

2.2疲劳前后橡胶SEM分析
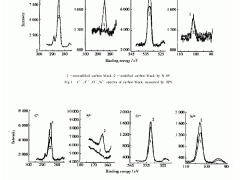
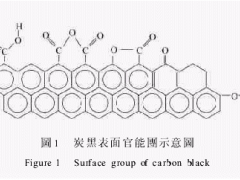
炭黑一次聚结体的尺寸大约在0.2μm左右,其二次聚集体大约为5~100μm[6],因此可用SEM来观测炭黑形态在疲劳前后的变化。如图3所示,图A为天然橡胶疲劳前断面上炭黑的形态,图B为经受20万次疲劳后在应力方向断面上炭黑的形态。

正如图3A所示,天然橡胶内部存在着大量的炭黑二次聚集体(a),图3B为试样经过20万次拉伸疲劳之后在拉伸方向上的SEM图像。从颗粒尺寸上看,二次聚集体体积及数量均大大减少(d),可以观察到大量的一次聚结体(c)并产生了微细孔洞(b),这说明炭黑二次聚集体在疲劳过程中发生了破坏。图中可以很清晰地看出,橡胶在拉伸方向上发生了取向,同时,仍存在的炭黑二次聚集体也发生了一定程度的取向。因此可以推测,炭黑二次聚集体的破坏是由于附着在其表面的橡胶在循环应力作用下发生了移动,牵引原本松散的炭黑二次聚集体分开。
2.3基于炭黑分散程度的橡胶疲劳破坏模型
上文叙述了炭黑分散程度对橡胶疲劳性能的影响。现从橡胶分子链滑动模型及橡胶疲劳破坏断裂力学唯象理论出发,提出了一个基于炭黑分散程度对橡胶疲劳性能影响的橡胶疲劳破坏模型(见图4)。

该模型认同橡胶分子链滑动模型理论关于补强的看法[7],即认为分子链能够在炭黑表面上滑动,形成了一种由炭黑构成节点的网络结构,该网络结构能够均匀地分布应力,从而达到补强的目的。而对于包括硫化胶在内的任何固体来说,其内部都必然含有分布于各处的不同形状和大小的缺陷[8]。当橡胶整体受力时,这些缺陷部位所受应力达到极大值,从而产生断链(过程A),由分子链断裂而产生的大分子自由基能与其临近的表面活性极大的炭黑结合。假若周围填料处于理想分散状态,则断裂的大分子链与其结合后重新形成网络结构,仍能继续承担加载的应力(过程B)。若周围填料成附聚体状态,则大分子链末端与其结合后(过程C)在应力作用下会发生附聚体的解聚(过程D),致使原分子链不能够继续承担应力,处于失效状态。当失效的大分子链达到一定数量时,就发生了宏观破坏,材料开始失效。
2.4模型合理性分析
断裂力学唯象理论[9]认为,橡胶材料的疲劳破坏主要是由于在外力作用下,橡胶内部的缺陷或微细裂纹引发的大裂纹不断传播和扩展所致。由于内部缺陷总是存在的,因此,可以认为裂纹的扩展速率是橡胶疲劳的控速步骤,可以想象,若顶端应力在疲劳过程中被耗散掉,则橡胶材料的抗疲劳性能会大大增强。在A阶段,大分子链的断裂会消耗掉一部分外界输入的能量。在B阶段断裂的分子链重新承载应力,这种耗散应为“良性耗散”,即只消耗能量却不影响分子链承载应力的能力。对于C过程来说,实际上是将应力转移至其它未断裂的分子链,增大了其断裂的可能性,这是“恶性耗散”。另外,从疲劳前后的SEM图像可以看出,炭黑二次聚集体只是炭黑一次聚结体松散的堆积,当其在应力作用下“被拉开”之后,可能会产生一些孔洞,而这些孔洞无疑进一步加速了橡胶材料的破坏过程。
本模型实际上认同以下基本关系,即炭黑初级粒子之间的作用力>大分子链中C—C键能>炭黑一次聚结体之间相互作用力。关于这一点可以从相关文献及实验结果中找到根据。
Bandyopadhyaya R[10]采用一种特制的纳米结构操纵装置,研究了聚合物/炭黑复合薄膜的纳米断裂行为,观察到薄膜本身先出现破坏,其次才是炭黑粒子链被拉断,即证明炭黑粒子链强度>C—C键的强度。Payne效应作为衡量炭黑在橡胶中微观分散的一种方法已被大家广泛认同,其在高应变下模量的下降源于炭黑二次聚集体的破坏。从图1来看,对混炼胶施加10%左右的剪切应变,炭黑二次聚集体发生破坏,这说明了炭黑一次聚结体之间作用力很小,至少小于C—C键的强度,故该模型所认同的基本关系成立。关于橡胶大分子在周期性应力下会发生断链而产生自由基,文献中已有报道[8]。需要说明的是,大分子链断开以后与临近炭黑相结合只是大分子自由基一种可能的结果,当然,可能还存在着大分子自由基与其他杂质(如空气中的氧等)发生反应而终止等情况。因此,即使填料呈理想分散状态,在足够长时间和施加周期性应力的情况下,橡胶仍会发生宏观破坏而失效。事实上,橡胶疲劳破坏是一个复杂的过程,与材料性质、加载应力、实验环境等均有很强的相关性,可能还包括臭氧氧化等化学反应[11-14]。因此,本模型只能定性地说明填料分散程度对橡胶材料疲劳性能的影响。
3·结语
本文提出的基于炭黑分散程度对填充橡胶疲劳寿命影响的模型确实符合众多实验事实,具有其合理性,能够定性地解释炭黑分散程度对疲劳寿命的影响方式,但橡胶疲劳是一个非常复杂的过程,对疲劳寿命的研究还要从多方面予以考虑。
参考文献:略